A binary search tree, sometimes called an ordered or sorted binary tree is a binary tree in which nodes are ordered in the following way:
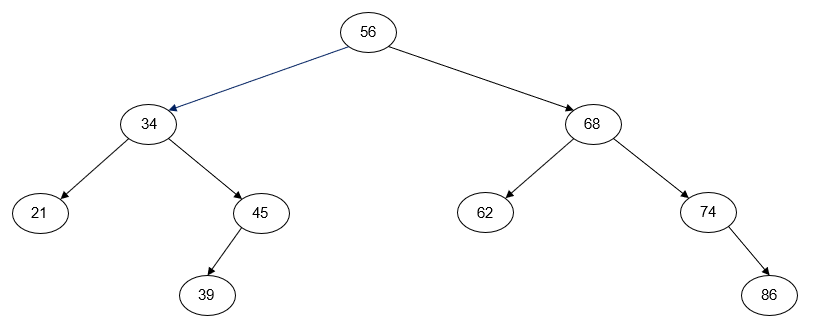
Figure 1: A Binary Search Tree

Performing a left-to-right inorder traversal of a binary search tree will "visit" the nodes in ascending key order, while performing a right-to-left inorder traversal will "visit" the nodes in descending key order.
Binary search trees are a common choice for implementing several abstract data types, including Ordered Set, Ordered Multi-Set, Ordered Map, and Ordered Multi-Map. These ADTs have three main operations:
Insertion into a binary search tree can be coded either iteratively or recursively. If the tree is empty, the new element is inserted as the root node of the tree. Otherwise, the key of the new element is compared to the key of the root node to determine whether it must be inserted in the root's left subtree or its right subtree. This process is repeated until a null link is found or we find a key equal to the key we are trying to insert (if duplicate keys are disallowed). The new tree node is always inserted as a leaf node.
Pseudocode for an iterative version of this algorithm is shown below.
Iterative Insertion into a Binary Search Tree Pseudocode
procedure insert(key : a key to insert, value : a value to insert)
// root : pointer to the root node of the tree (nullptr if tree is empty)
// t_size : tree size
// p : pointer to a tree node
// parent : pointer to the parent node of p (nullptr if p points to the root node)
// new_node : pointer used to create a new tree node
// Start at the root of the tree.
p ← root
parent ← nullptr
// Search the tree for a null link or a duplicate key (if duplicates are disallowed).
while p != nullptr and key != p->key
parent ← p
if key < p->key
p ← p->left
else
p ← p->right
end if
end while
// If duplicates are disallowed, signal that insertion has failed.
if p != nullptr
return false
end if
// Otherwise, create a tree node and insert it as a new leaf node.
Create a new tree node new_node to contain key and value
if parent == nullptr
root ← new_node
else
if new_node->key < parent->key
parent->left ← new_node
else
parent->right ← new_node
end if
end if
t_size ← t_size + 1
// If duplicates are disallowed, signal that insertion has succeeded.
return true
end procedureBinary Search Tree Insertion Example
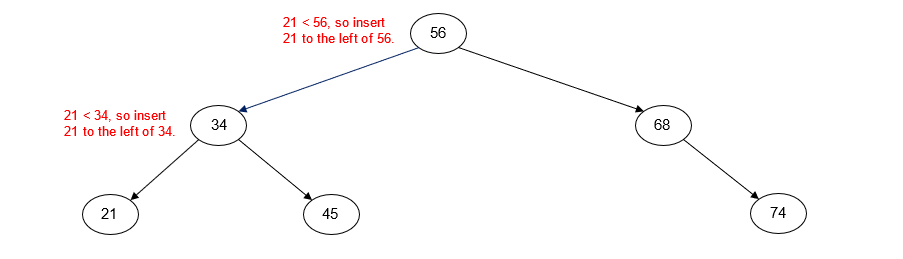
Insert 56 into empty tree

Insert 34

Insert 45
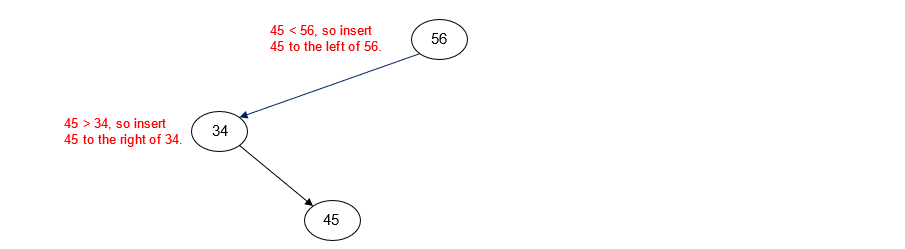
Insert 68
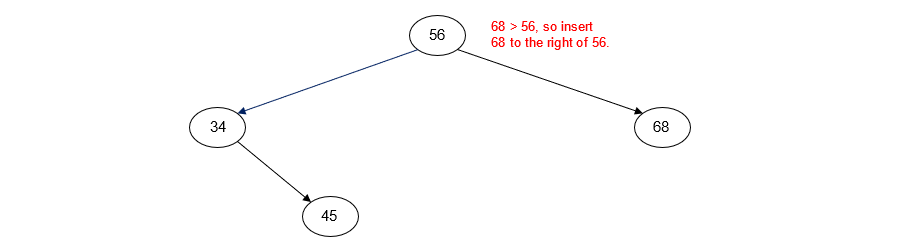
Insert 74
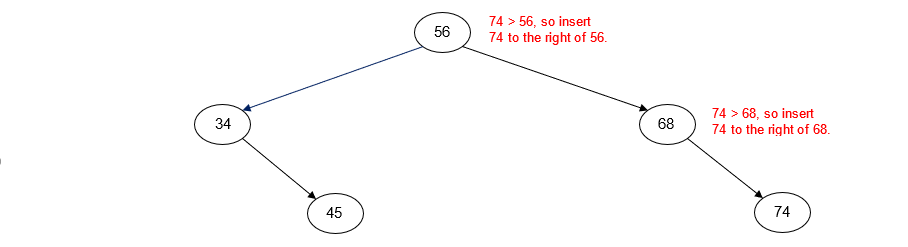
Insert 21
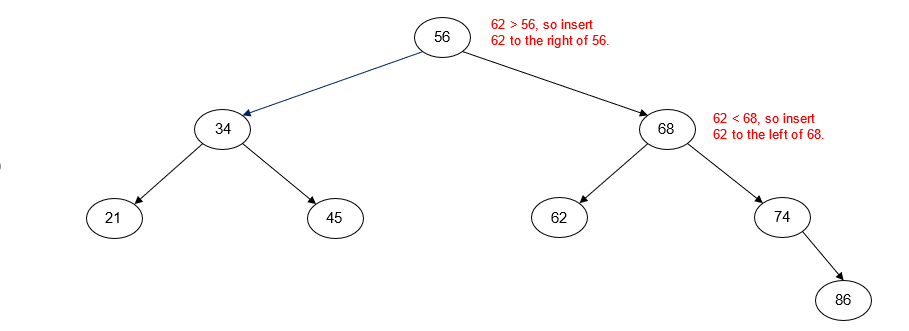
Insert 86

Insert 62
Insert 39
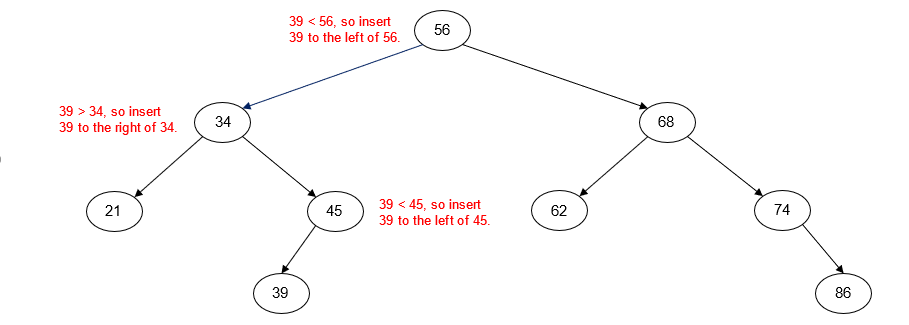
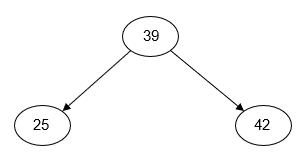
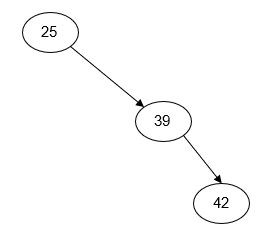
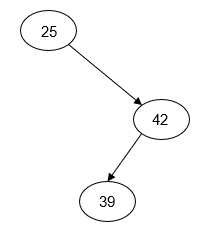
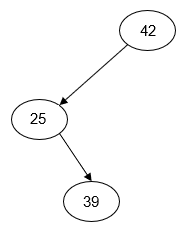
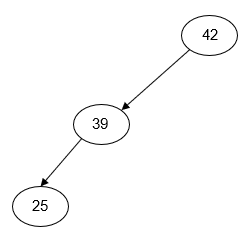
As the example above illustrates, the arrangement of the nodes in a binary search tree depends entirely on the order in which the keys are inserted. For example, if we insert the keys 25, 39, and 42, we could end with any one of five different node arrangements depending on the order in which the keys are inserted:
Figure 2: Alternate Binary Search Tree Arrangments
| Insert: 39, 25, 42 | Insert: 39, 42, 25 | Insert: 25, 39, 42 |
|---|---|---|
 |
 |
 |
| Insert: 25, 42, 39 | Insert: 42, 25, 39 | Insert: 42, 39, 25 |
 |
 |
 |
All of the trees shown above will produce the same output when traversed using the inorder traversal algorithm.
As the third diagram in each of the rows of Figure 2 shows, if keys are inserted into a binary search tree in sorted order, they will always end up being inserted in the same subtree. The result is referred to as a degenerate binary search tree and is effectively a linked list. This has a negative impact on the complexity of the binary search tree operations (see Complexity below). One way to prevent this problem is with a self-balancing binary search tree such as an AVL tree or a red-black tree. Both data structures are outside the scope of this course.
Deletion of a node with a specified key from a binary search tree can also be coded either iteratively or recursively. Pseudocode for an iterative version of the algorithm is shown below.
Iterative Deletion from a Binary Search Tree Pseudocode
procedure remove(key : key to remove from the tree)
// root : pointer to the root of the binary search tree
// t_size : tree size
// p : pointer to the node to delete from the tree
// parent : pointer to the parent node of the node to delete from the tree (or
// nullptr if deleting the root node)
// replace : pointer to node that will replace the deleted node
// replace_parent : pointer to parent of node that will replace the deleted node
// Start at the root of the tree and search for the key to delete.
p ← root
parent ← nullptr
while p != nullptr and key != p->key
parent ← p
if key < p->key
p ← p->left
else
p ← p->right
end if
end while
// If the node to delete was not found, signal failure.
if p == nullptr
return false
end if
if p->left == nullptr
// Case 1: p has not left child. Replace p with its right child.
replace ← p->right
else if p->right == nullptr
// Case 2: p has no right child. Replace p with its left child.
replace ← p->left
else
// Case 3: p has two children. Replace p with its inorder predecessor.
// Go left...
replace_parent ← p
replace ← p->left
// ...then all the way to the right.
while replace->right != nullptr
replace_parent ← replace
replace ← replace->right
end while
// If we were able to go to the right, make the replacement node's
// left child the right child of its parent. Then make the left child
// of p the replacement's left child.
if replace_parent != p
replace_parent->right ← replace->left
replace->left ← p->left
end if
// Make the right child of p the replacement's right child.
replace->right ← p->right
end if
// Connect replacement node to the parent node of p (or the root if p has no parent).
if parent == nullptr
root ← replace
else
if p->key < parent->key
parent->left ← replace
else
parent->right ← replace
end if
end if
// Delete the node, decrement the tree size, and signal success.
Delete the node pointed to by p
t_size ← t_size - 1
return true
end procedureBinary Search Tree Deletion Examples
The following diagrams illustrate the three cases that can be encountered when deleting a node from a binary search tree.
Node to delete has no left child
When a node we want to delete has no left child, we replace the deleted node with its right child. If the node to delete also has no right child, it will be replaced with nullptr.
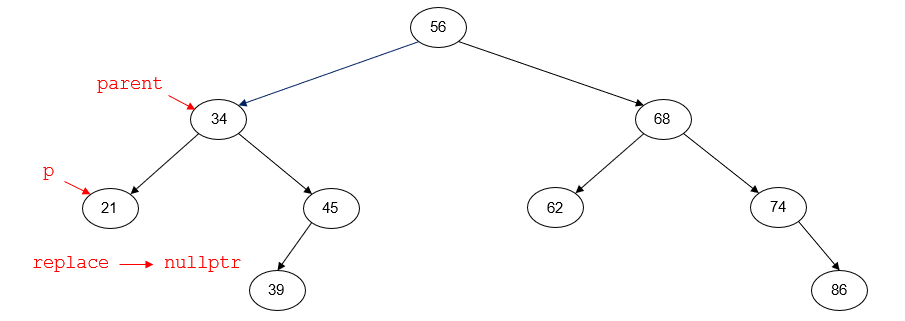
For example, suppose that we want to delete the node with key 21. Prior to deleting the node, the tree will look like the following diagram. p points to the node to be deleted (21). parent points to
the parent node of p (34). replace is set to p->right; since the node with key 21 has no right child, replace will be nullptr.
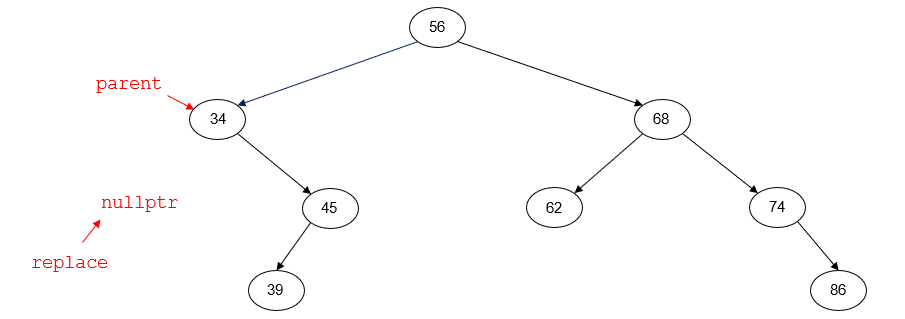
After deletion, the tree will look like this:
On the other hand, if the node we want to delete does have a right child, the deleted node is replaced with that right child.
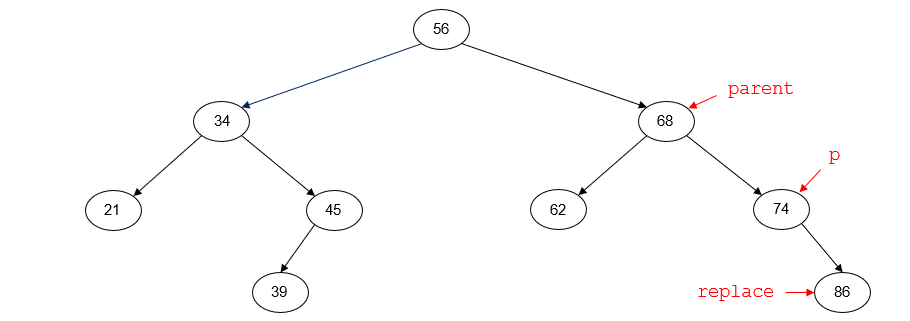
For example, suppose that we want to delete the node with key 74. Prior to deleting the node, the tree will look like the following diagram. p points to the node to be deleted (74). parent points to
the parent node of p (68). replace points to the right child of p (86).
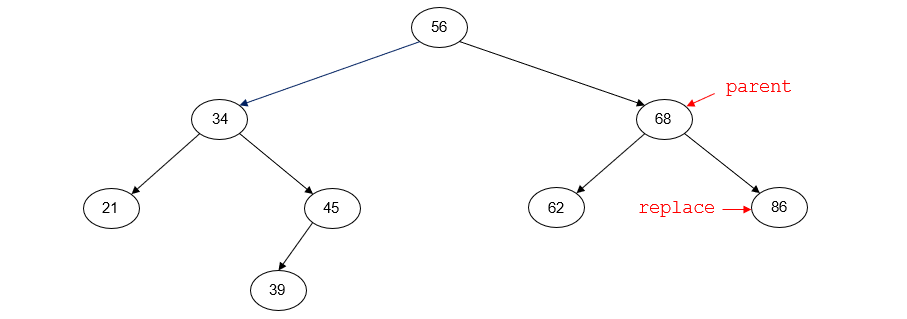
After deletion, the tree will look like this:
Node to delete has no right child
When a node we want to delete has no right child, we replace the deleted node with its left child.
For example, suppose that we want to delete the node with key 45. Prior to deleting the node, the tree will look like the following diagram. p points to the node to be deleted (45). parent points to
the parent node of p (34). replace points to the left child of p (39).
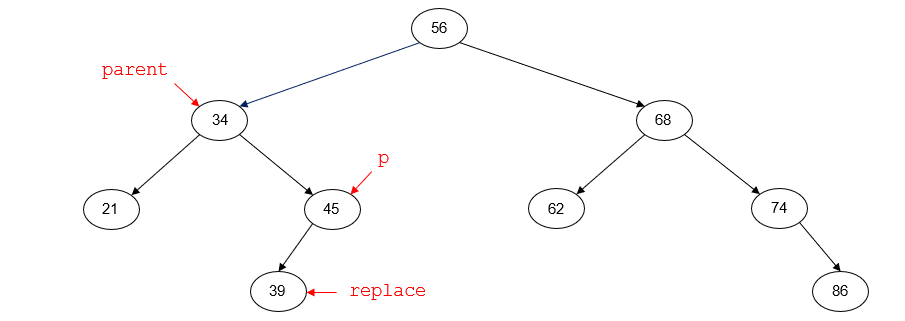
After deletion, the tree will look like this:
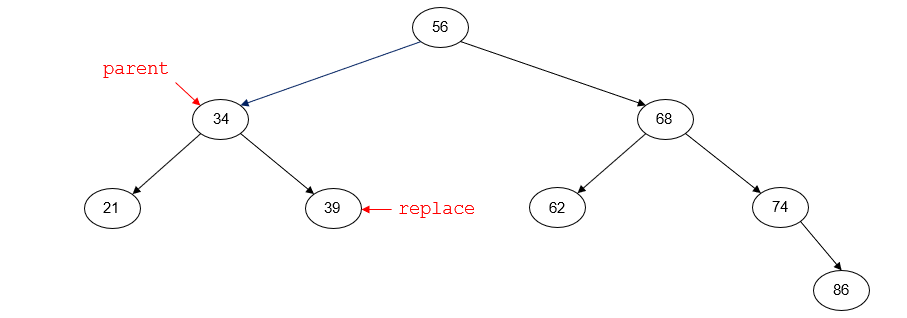
Node to delete has two children
When a node to delete has no right child, we replace the deleted node with its inorder predecessor. (Replacing the node with its inorder successor would also work, but we have to pick one or the other when we code the algorithm.) To find the inorder predecessor of a node with two children, we go to its left and then all the way to the right.
Sometimes after going left we may be unable to go right, because the left child of p has no right child. In that case, the left child of p is its inorder predecessor.
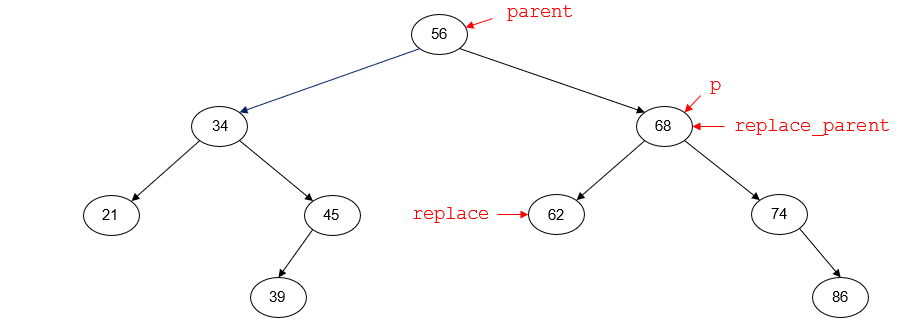
For example, suppose that we want to delete the node with key 68. Prior to deleting the node, the tree will look like the following diagram. p points to the node to be deleted (68). parent points to
the parent node of p (56). replace points to the left child of p (62), which is its inorder predecessor. replace_parent points to the same node as p (68), which
tells us that after going left we were unable to go to the right.
We know in this situation that the node pointed to by replace is the left child of p, so we don't need to worry about dealing with that. The node pointed to by p also has a right
child. Since the node pointed to by replace currently has no right child of its own (remember, we were unable to go to the right), the right child of the node pointed to by p can become its new right
child.
After deletion, the tree will look like this:
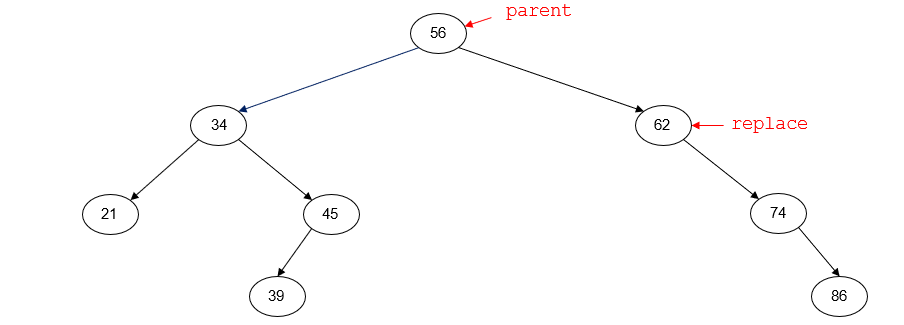
If the left child of p has a right child, we need to continue going to the right until we reach a node with no right child. That node will be the inorder predecessor of p.
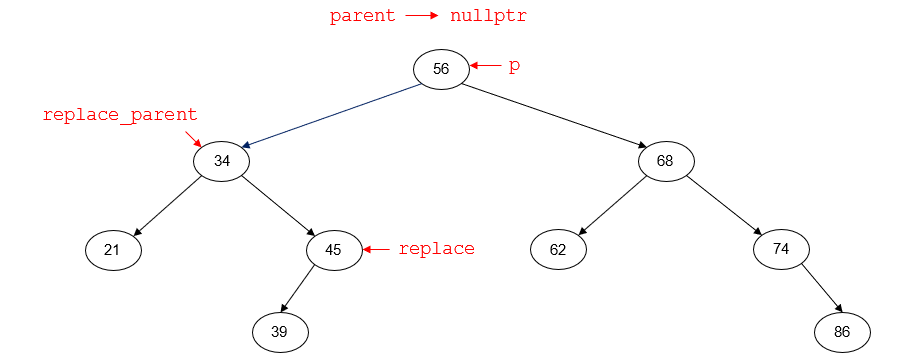
For example, suppose that we want to delete the node with key 56. Prior to deleting the node, the tree will look like the following diagram. p points to the node to be deleted (56). parent is nullptr;
the node with key 56 is the root node of the tree and has no parent node. replace points to the inorder predecessor of p (45). replace_parent points to the parent node of
replace (34).
In this situation, we have a couple more links that need to be set. The node pointed to by replace has no right child, but it might have a left child. That left child will become the right child of replace_parent, taking
the place of the node pointed to by replace.
The node pointed to by p definitely has both a left child and a right child - if it didn't, we wouldn't be in the code for this case! Those children need to become the children of the node pointed to by
replace.
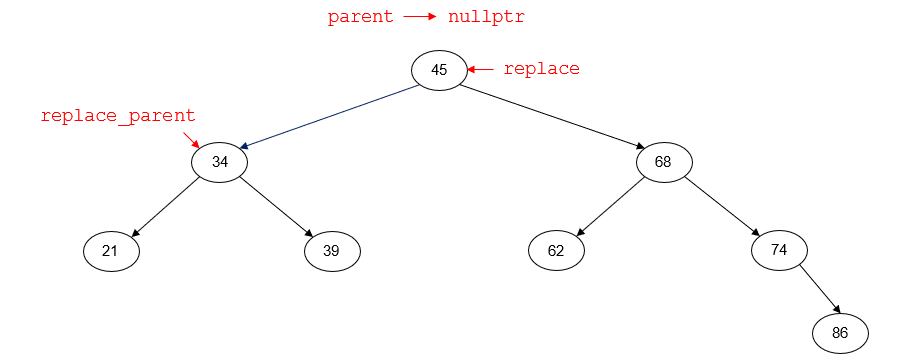
After deletion, the tree will look like this:
The find or lookup operation can be coded either iteratively or recursively. Pseudocode for an iterative version of this algorithm is shown below.
procedure find(key : a key for which to search)
// root : pointer to the root node of the tree (nullptr if tree is empty)
// p : pointer to a tree node
// Start at the root of the tree.
p ← root
// Search the tree for a null link or a matching key.
while p != nullptr and key != p->key
if key < p->key
p ← p->left
else
p ← p->right
end if
end while
// p either points to the node with a matching key or is nullptr if
// the key is not in the tree.
return p
end procedureAlternatively, this algorithm can simply return true if the search key is found, and false if it is not found.
We can code a linked binary search tree as a struct and a class in C++.
Sample template struct to represent a tree node
template <class K, class V>
struct node
{
K key;
V value;
node<K, V>* left;
node<K, V>* right;
node(const K& key = K(), const V& value = V(), node<K, V>* left = nullptr, node<K, V>* right = nullptr)
{
this->key = key;
this->value = value;
this->left = left;
this->right = right;
}
};
Class to represent a binary search tree
Data members
node<K, V>* root - Root pointer. Points to the root node of the tree or is nullptr if the tree is empty.t_size - Tree size. The number of items currently stored in the binary search tree.Member Functions
The insert(), remove(), and find() have already been described in detail.
Any of the binary tree traversals (particularly inorder traversal) may be also be coded as member functions of the class. Other common member functions are described
below.
Default constructor
Sets tree to initial empty state. The root node pointer should be set to nullptr. The tree size should be set to 0.
size()
Returns the tree size.
empty()
Returns true if the tree size is 0; otherwise, false.
clear()
Sets the tree back to the empty state.
procedure clear()
destroy(root)
root ← nullptr;
t_size ← 0
end procedure
destroy()
Recursively deletes the nodes of a bstree object. This is a modified version of a postorder traversal of the tree.
procedure clone(p : pointer to a tree node)
if p != nullptr
// Recursively destroy the left and right subtrees of the node pointed to by p.
destroy(p->left)
destroy(p->right)
Delete the node pointed to by p
end if
end procedure
Copy Constructor
procedure bstree(x : reference to a constant bstree)
// Copy the other bstree object's size
t_size ← x.t_size
// Copy the nodes of the other bstree object
root = clone(x.root)
end procedure
Copy Assignment Operator
procedure operator=(x : reference to a constant bstree)
if this != &x
// Make the left bstree object empty
clear()
// Copy the other bstree object's size
t_size ← x.t_size
// Copy the nodes of the other bstree object
root = clone(x.root)
end if
return *this;
end procedure
Destructor
We can delete all of the dynamic storage for the tree by calling the clear() member function.
clone()
Recursively copies the nodes of a bstree object. This is a modified version of a preorder traversal of the tree.
procedure clone(p : pointer to a tree node)
if p != nullptr
// Make a copy of the node pointed to by p.
Allocate a new tree node, new_node
new_node->key ← p->key
new_node->value ← p->value
// Recursively copy the left and right subtrees of the node pointed to by p.
new_node->left ← clone(p->left)
new_node->right ← clone(p->right)
return new_node
else
return nullptr
end if
end procedure
The time complexity for the insertion, deletion, and find / lookup operations is based on the height of the binary search tree. For a complete or almost complete binary tree, the time complexity of these operations will be O(log n) - we eliminate one of a node's two subtrees from consideration with each key comparison. In the case of a degenerate binary search tree, the time complexity of these operations will be no better than they would be for a linked list - i.e., O(n).
Space complexity for the iterative implementations of these operations will be O(1). For recursive implementations, the space complexity will be similar to the time complexity.
The time complexity for traversals of the tree will always be O(n), since we "visit" every node in the tree. This also includes the clone() and destroy() functions described
above, which are called by the copy constructor, copy assignment operator, and destructor.
Space complexity for traversals of the tree is generally based on the height of the tree. For a complete or almost complete binary tree, the space complexity of a traversal will be O(log n), while a traversal of a a degenerate binary search tree will have a space complexity of O(n).